Abstract
We’ll now see explicitly how to find the set of (mixed-strategy) Nash equilibria for general two-player games where each player has a strategy space containing two actions (i.e. a “2×2 matrix game”).
We first compute the best-response correspondence for a player. We partition the possibilites into three cases: The player is completely indifferent; she has a dominant strategy; or, most interestingly, she plays strategically (i.e., based upon her beliefs about her opponent’s play).
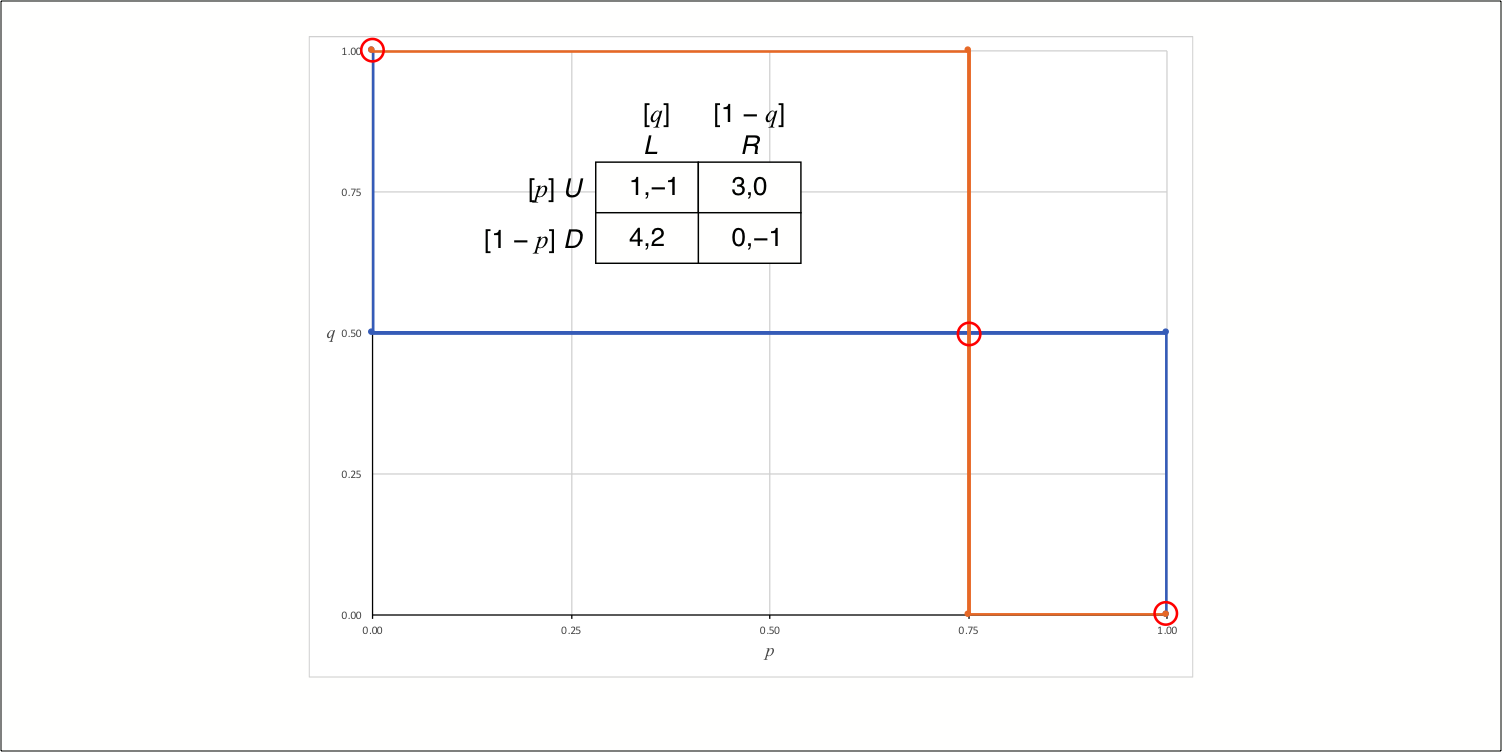
The Nash equilibria of the game are the strategy profiles in the intersection of the two players’ best-response correspondences. We use this fact and the possible forms of players’ best-response correspondences to explore the possible sets of Nash equilibria in these games.
We then apply this technique to two particular games. The first game is a typical and straightforwardly solved example; the second is nongeneric in the sense that it has an infinite number of equilibria. For each game we will compute the graph of each player’s best-response correspondence and identify the set of Nash equilibria by finding the intersection of these two graphs.






