Abstract
We consider here the simplest dynamic games of incomplete information: sender-receiver games. There are only two players: a Sender (S) and a Receiver (R). The Sender’s action will be to send a message, m, chosen from a message space M to the Receiver. The Receiver will observe this message m and respond to it by choosing an action a from his action space A.
To make this game a simple but nontrivial game of incomplete information we endow the Sender with some private information which we describe by her type. The Receiver has no private information, so he has but a single type, which we then have no need to mention further. The Receiver does have prior beliefs (i.e. prior to observing the Sender’s message) about the Sender’s type, which are described by the probability distribution over the Sender’s type space. After the Receiver takes an action a, each player is awarded a payoff which can in general depend on the message m the Sender sent, the action a the Receiver took in response, and the type which Nature chose for the Sender. We can express this game of incomplete information as an extensive-form game of imperfect information by explicitly representing Nature, who chooses a type for the Sender.
A strategy for the Sender is a specification of a message (or distribution over messages) for each Sender type. A strategy for the Receiver is a pure or mixed action in response to each possible message in the message space. After observing the Sender’s message, the Receiver will update his beliefs about the type of the Sender, using Bayes’ Rule when possible.
A Bayesian equilibrium of the sender-receiver game is (a) a strategy for each type of Sender, (b) a strategy for the Receiver, and (c) a conditional posterior belief system describing the Receiver’s updated beliefs about the Sender’s type as a function of the observed message, which satisfies two optimality conditions and a Bayes-consistency condition. Each Sender type’s message must be optimal given the anticipated reaction by the Receiver. The Receiver’s strategy must choose, for each “on the path” message, an action that is optimal given the Receiver’s updated posterior beliefs about the Sender’s type. And the Receiver’s conditional posterior belief system must be consistent with Bayes’ Rule whenever possible (i.e., on the equilibrium path). Perfect Bayesian equilibrium strengthens the Receiver-optimality condition to apply to off-the-path messages as well.
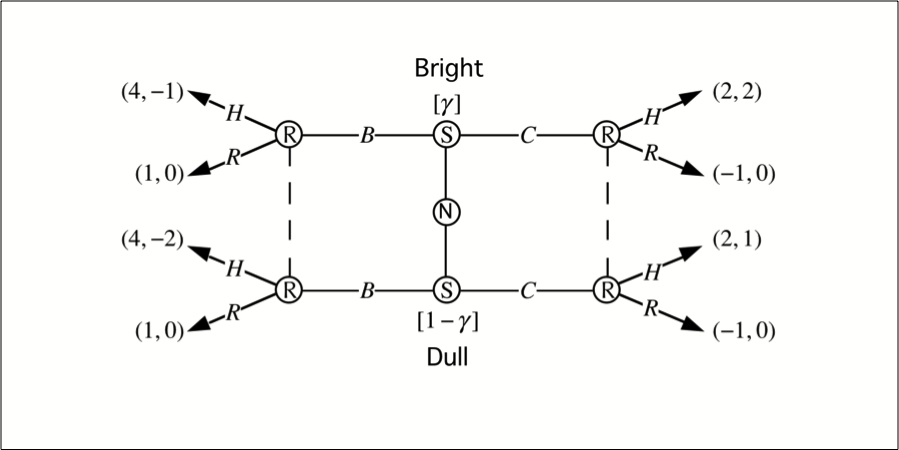
An example sender-receiver game motivates the claim that Perfect Bayesian equilibria can still be undesirable. Two additional refinements are considered and applied to example games: The Test of Dominated Messages, and the Intuitive Criterion.






