Abstract
In many economically important situations the game may begin with some player having private information about something relevant to her decision making. These are called games of incomplete information, or Bayesian games. (Incomplete information is not to be confused with imperfect information, in which players do not perfectly observe the actions of other players.) Although any given player does not know the private information of an opponent, she will have some beliefs about what the opponent knows, and we will assume that these beliefs are common knowledge.
In many cases of interest we will be able to model the informational asymmetry by specifying that each player knows her own payoff function, but that she is uncertain about what her opponents’ payoff functions are.
We will introduce the notion of a player’s type to describe her private information. A player’s type fully describes any information she has which is not common knowledge. Each player knows her own type with complete certainty. Her beliefs about other players’ types are captured by a common-knowledge joint probability distribution over the others’ types.
We can think of the game as beginning with a move by Nature, who to each player assigns a type. Nature’s move is imperfectly observed, however: each player observes the type which Nature has bestowed upon her, but no player directly observes the type bestowed upon any other player. We can think of the game which follows as a strategic-form game being played by a single type of each player, where at least one player doesn’t know which type of some other player she is facing.
A strategy for a player in the incomplete-information game is a strategy for each of that player’s types for the appropriate strategic-form game.
A Bayesian equilibrium of a static game of incomplete information is a strategy profile such that every type of every player is maximizing her expected utility given the type-contingent strategies of her opponents and the probability distribution over types of each player.
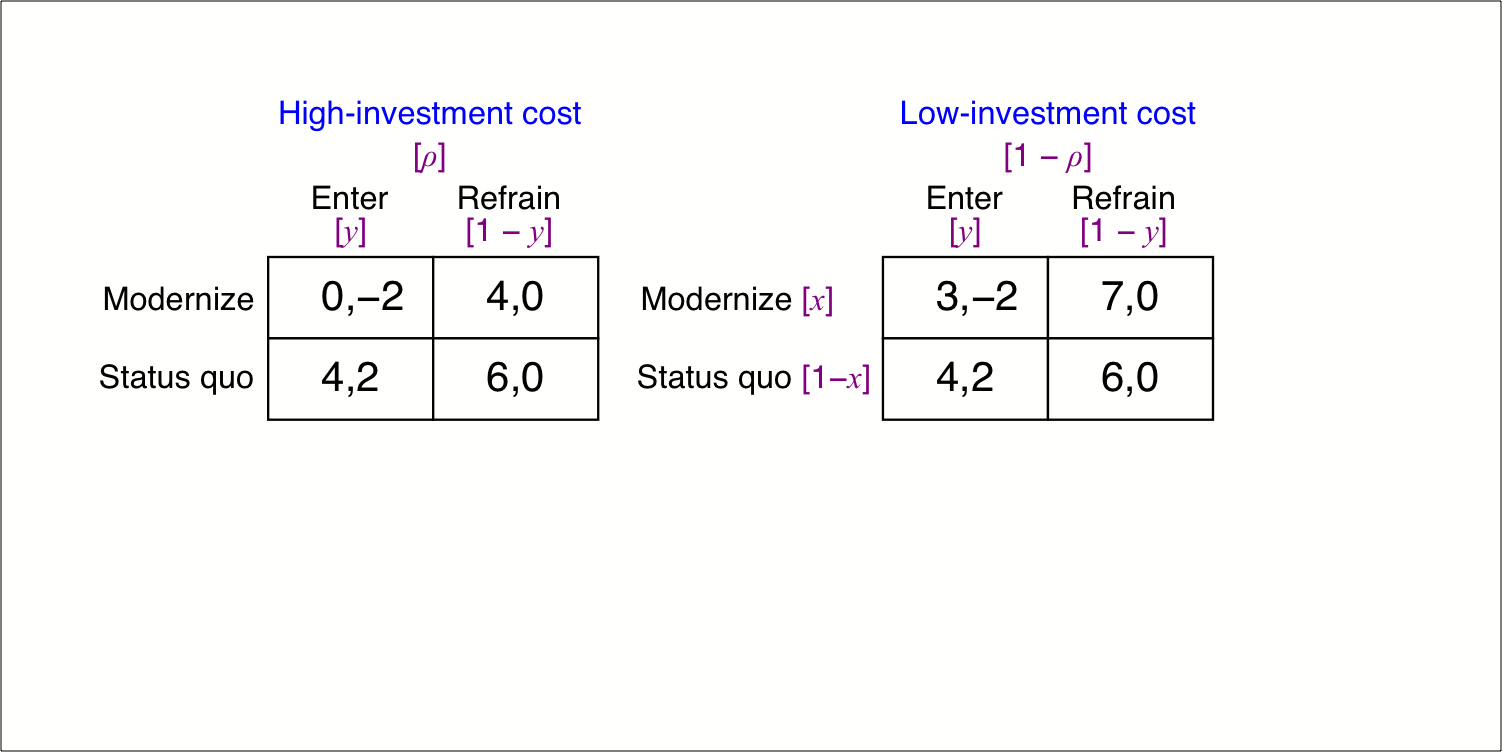
We consider an industrial-organization example with two firms, where one firm, the incumbent, knows privately whether its investment cost is low or high. We compute the Bayesian equilibrium to predict whether the challenger will enter the market and whether the incumbent firm will modernize its technology.






